https://doi.org/10.1016/j.matdes.2023.111644
感谢东北大学的王琪博士、董艳伍教授、姜周华教授对中材电镜中心的支持与认可!

推荐这篇论文,希望大家分享转发,参考引用!
经过Zr处理的Invar合金显示出足够低的热膨胀系数(CTE),残余应力的存在和晶粒的细化是导致CTE明显下降的原因;
加入Zr后的Invar合金,屈服强度从256MPa提高到401MPa,强化贡献主要来自于位错强化和晶粒细化强化;
含Zr的Fe-36Ni Invar合金更细小,位错密度明显增加;
在添加0.22% Zr的Fe-36Ni Invar合金中观察到两种类型富Zr金属间化合物,即Ni7Zr2和Ni2Zr,主要分布在晶界上,可抑制再结晶过程。
本文做透射电镜(TEM) 测试
测试目的如下:
一 在TEM下进一步验证热力学计算、XRD、SEM结果,能否观察到Ni7Zr2析出相?
此外,是否还有其他富Zr相?
二 富Zr相的分布区域?是否与SEM观察结果一致?其尺寸有多大?周围是否存在位错?对位错有何影响?
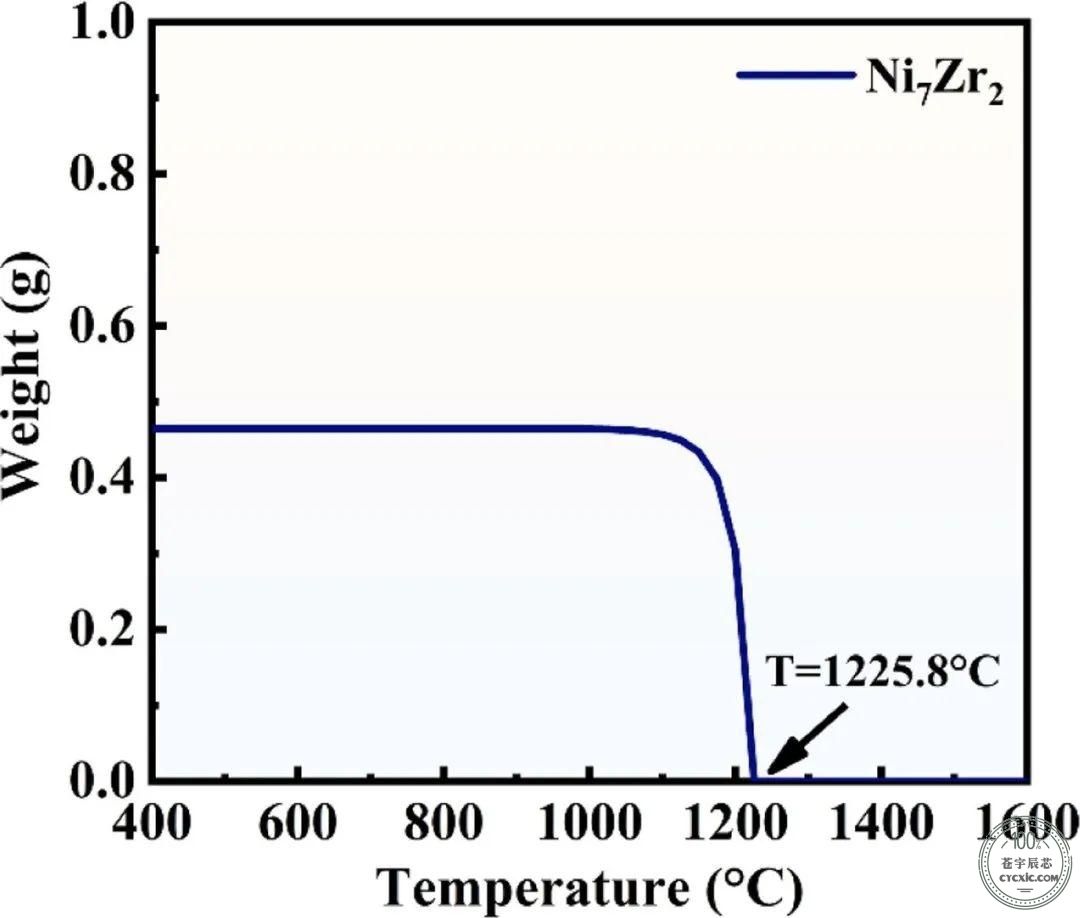
图1
使用FactSage软件对S2样品中主要形成的相进行热力学计算。
S1和S2分别代表未添加Zr的Fe-36Ni Invar合金,
添加0.22% Zr的Fe-36Ni Invar合金。
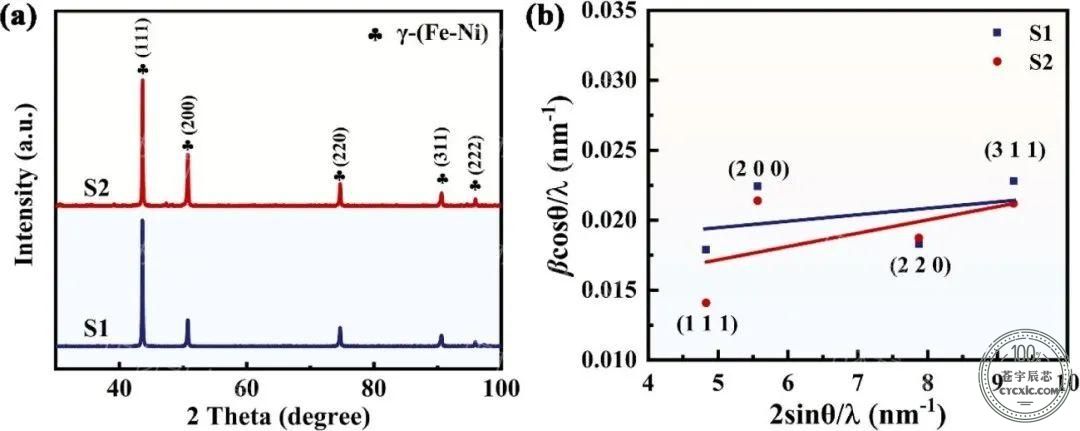
图2
(a) S1和S2合金的XRD图;
(b) βcosθ/λ和2sinθ/λ的关系图,线性拟合的斜率显示了ε的值。
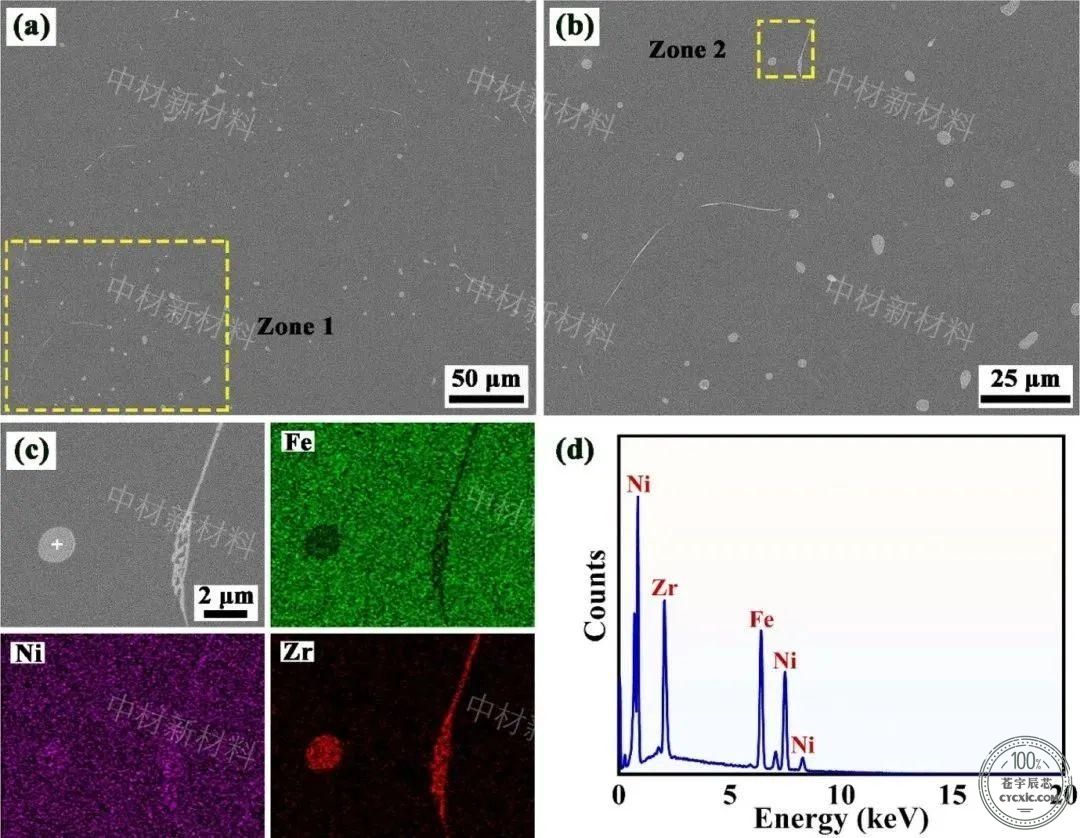
图3 S2合金中富含Zr的IMCs SEM-EDS结果。
(a)S2合金中富含Zr相的典型形态;
(b)-(a)中1区方框区域的放大图;
(c)-(b)中2区方框区域的SEM和EDS图;
(d)-(c)中光谱1的点分析图。
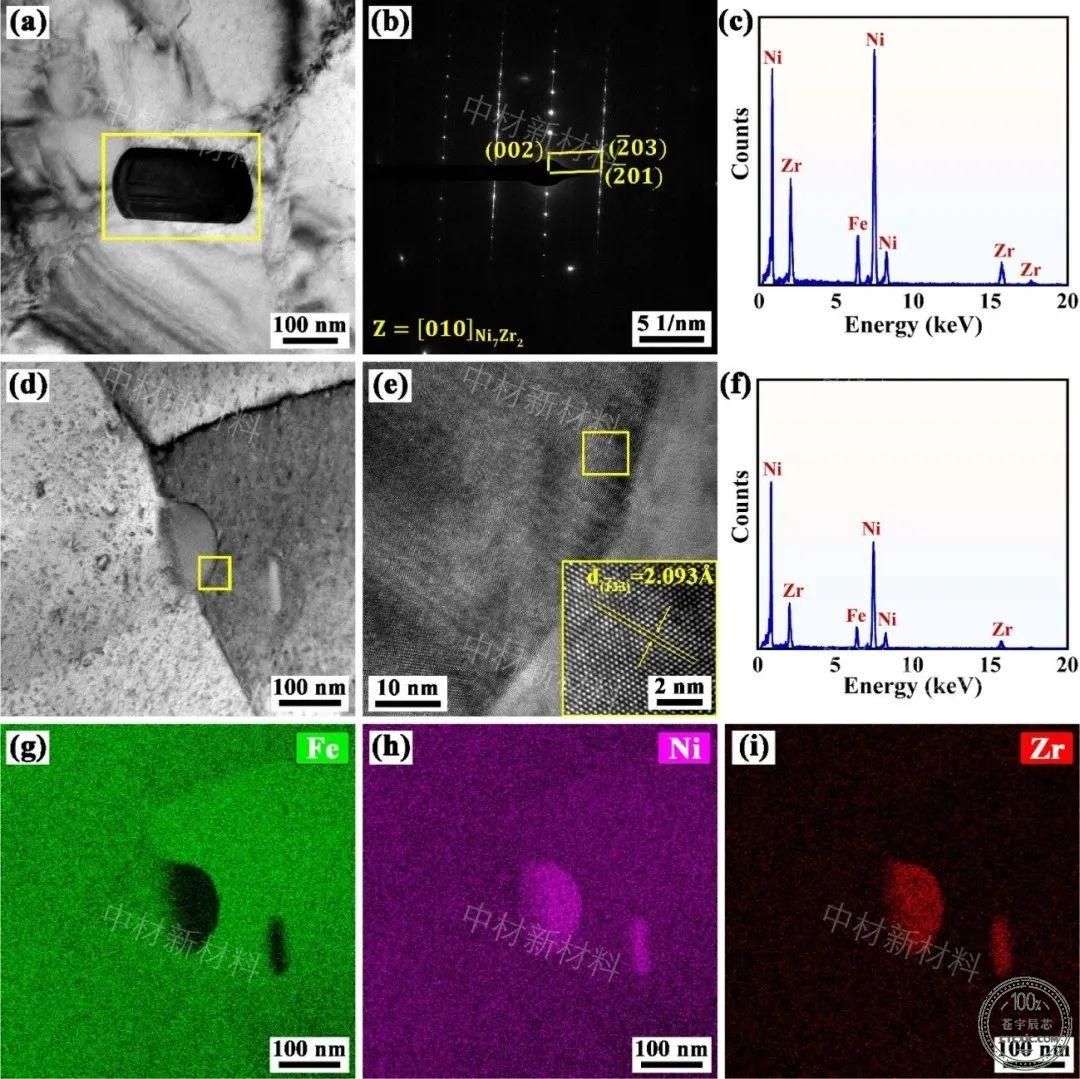
图4 S2合金中Ni7Zr2沉淀相的TEM分析。
(a)沉淀相的BF图像;(b)-(a)中标有黄框的Ni7Zr2相衍射图案;
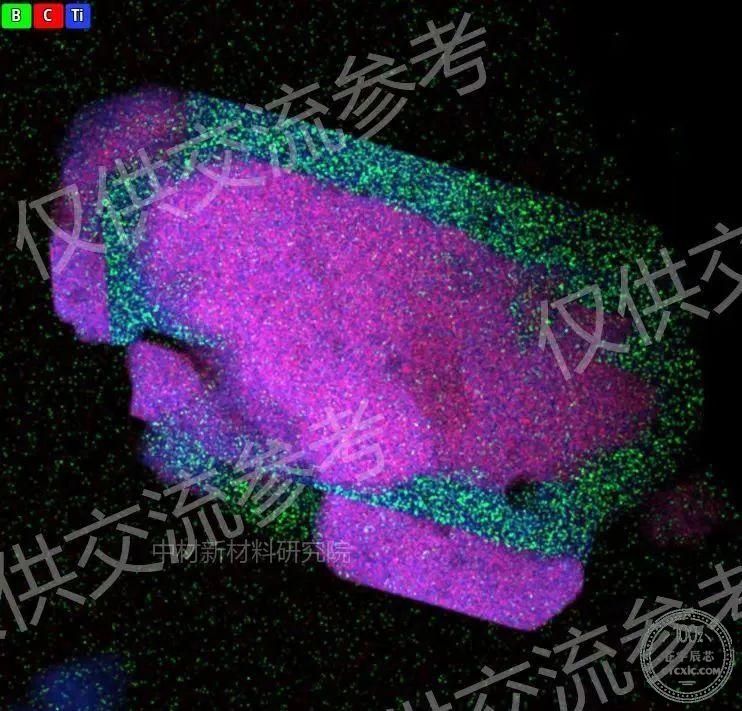
(c)-(a)中标有黄框的Ni7Zr2相能谱(EDS)。(d) 沉淀相的BF图像;(e)-(d)中标有黄框的Ni7Zr2相HRTEM图像;
(f)-(d)中标有黄框的Ni7Zr2 能谱;
(g)、(h)和(i)分别是(d)中相应的Fe、Ni和Zr组成图。
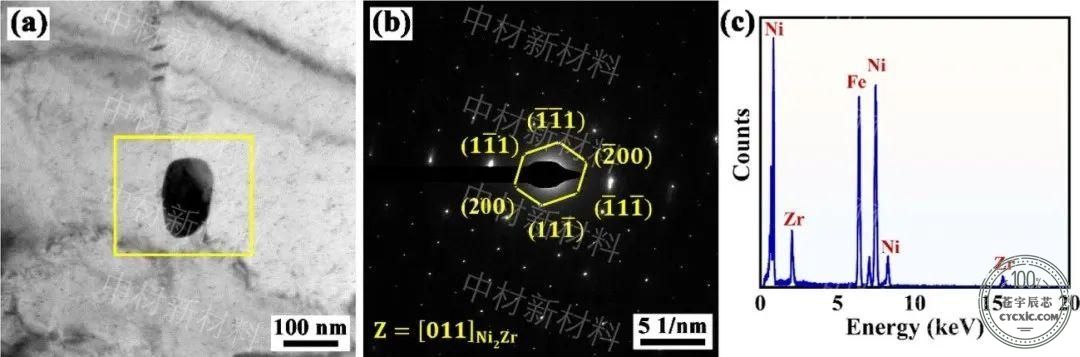
图5 Ni2Zr沉淀相的TEM分析。
(a) 沉淀相的BF图像;
(b) (a)中标有黄色方框的Ni2Zr相的相应衍射图案;
(c) (a)中标有黄色方框的Ni2Zr相的相应EDS。

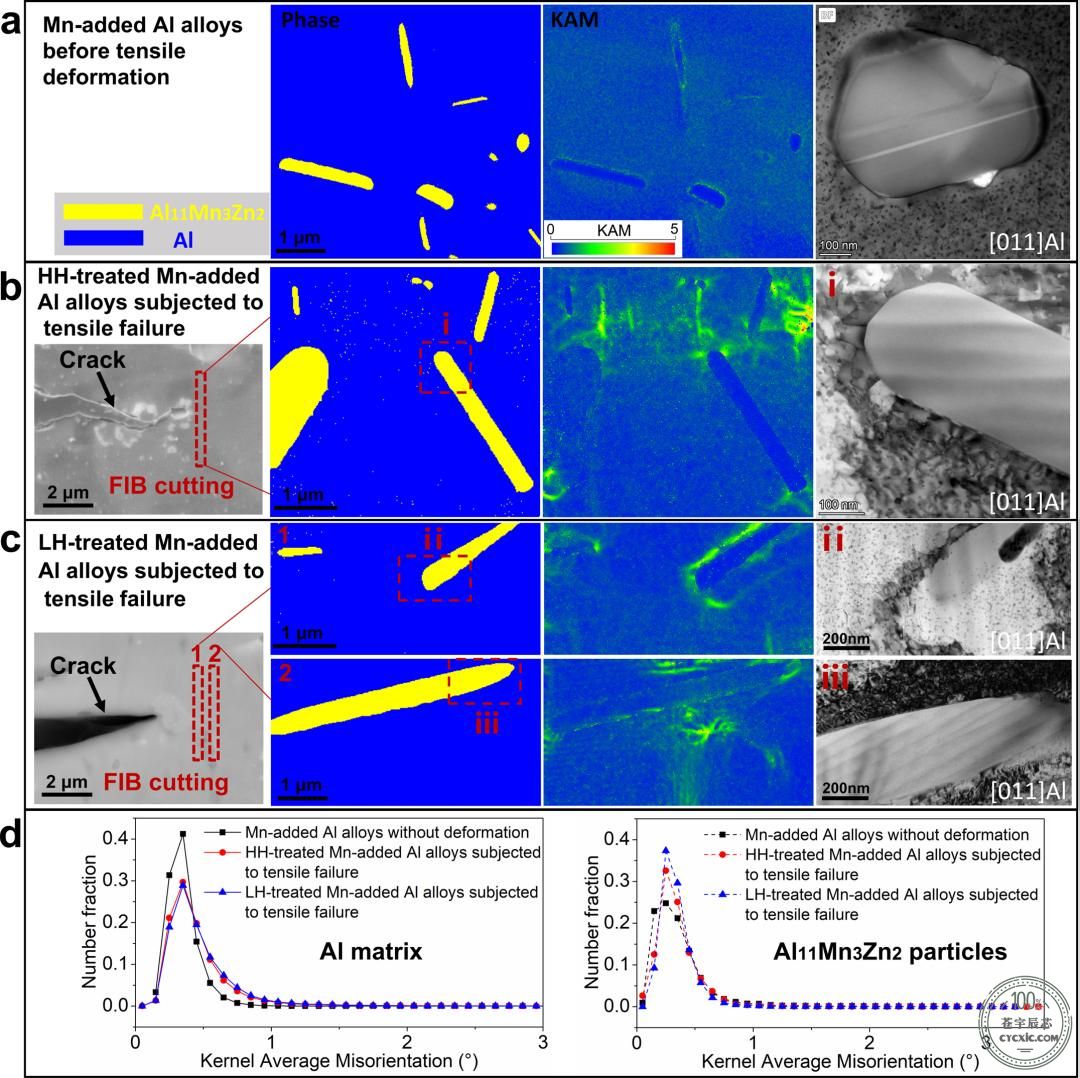
图6 S2合金的TEM图像。
(a)S2合金中的亚晶粒;
(b)富含Zr的IMC在位错处的钉扎作用;
(c)通过多边形化形成的回复组织;
(d)基体中富含Zr的IMC。
图4-6
透射电镜(TEM)测试结果主要表明
通过对透射电镜的SAED以及HRTEM结果分析并结合能谱,确认了Ni7Zr2、Ni2Zr沉淀相的存在;
Zr-Ni相的尺寸主要集中在50∼200μm范围内,平均晶粒尺寸为135μm。
文章中其他重要知识点
该方法先通过XRD测量出钢中的微观应变量和平均晶粒尺寸,再通过微观应变量、平均晶粒尺寸引起的衍射峰宽化的Williamson-Hall模型来计算出位错密度。
该方法的优点是对试样的制样要求较低,能较为准确的测定一块样品中的位错密度,并且能定量,是目前大家公认的较为可靠的一种方法。
假设内部应变只由位错产生,位错密度(ρ)用以下公式计算:
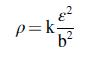
其中b是布尔格斯矢量(0.25纳米),k是一个几何常数,体心立方(bcc)材料的k = 14.4,面心立方(fcc)材料的k = 16.1。
以上公式,b、k是已知量,现主要是通过XRD确定ε值。
XRD半宽高β由两部分组成:微应变半宽高βS(由溶液原子或位错引起的晶格畸变)和晶粒尺寸半宽高βG。
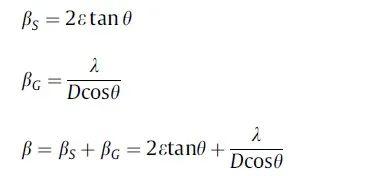
进一步转化公式:
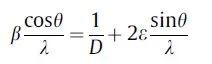
其中β是某些衍射峰的最大值半宽高值(FWHM),ε是微应变,θ是某些衍射峰的布拉格角,D是晶粒大小,λ是Cu Ka辐射的波长(λ = 0.15406 nm)。
当晶粒尺寸大于100纳米时,晶粒尺寸因素可以忽略不计。本文中奥氏体晶粒的尺寸是微米级的,因此,在衍射峰中的晶粒尺寸效应可以被忽略掉。简化公式:
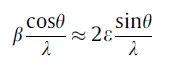
其中ε可以通过拟合不同衍射峰的βcosθ/λ和2sinθ/λ的斜率获得,如图2(b)所示。估计S1和S2合金的平均微应变系数ε分别为0.00048和0.00095左右。
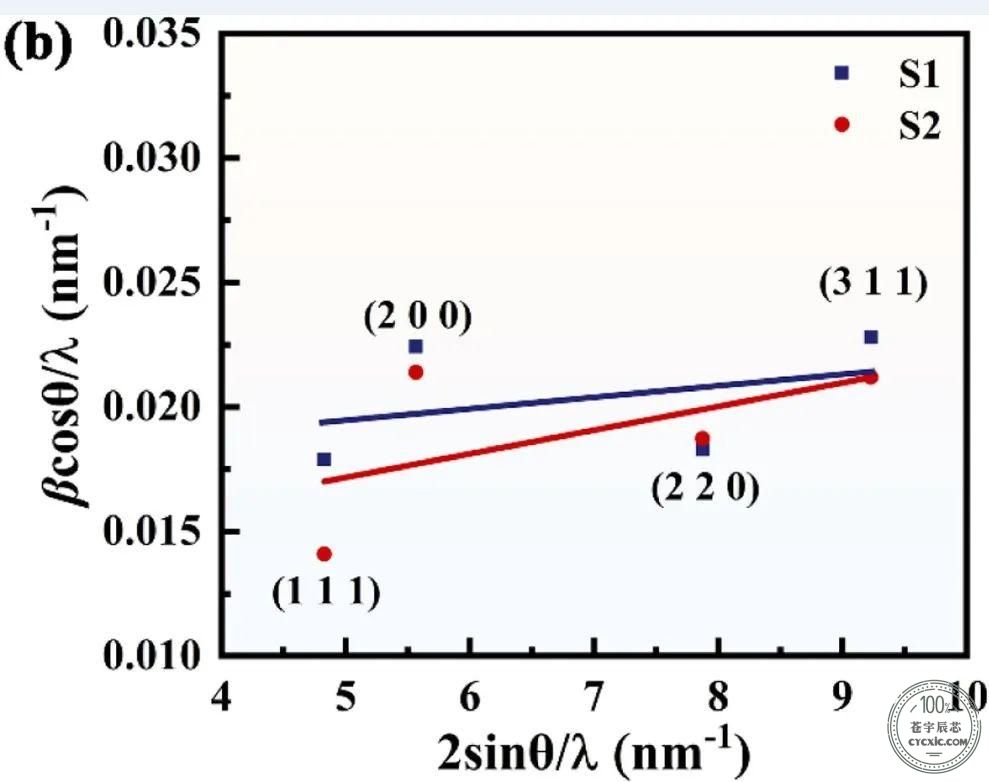
图2(b)
有了ε值,就可以通过下面公式来计算位错密度
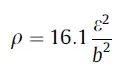
其中b是Burgers矢量(b≈2.5787 × 10-10 m)。根据上面公式,S1和S2合金的位错密度分别约为0.56 × 1014 m-2和2.19 × 1014 m-2。因此,相对于S1合金来说,S2合金的位错密度有明显的增加。
合金材料的主要强化成分是固溶强化(σs)、晶粒细化强化(σg)、位错强化(σd)和沉淀强化(σp)。屈服强度是四个单独贡献的总和,可表示为以下公式。
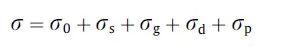
其中σ0是铁基体的固有强度,为53.9MPa。
晶粒细化对屈服强度的贡献可以通过霍尔-佩奇关系定量计算,如下面公式所示
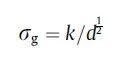
其中k代表霍尔-佩奇系数,对于奥氏体钢,k等于24.70MPamm1/2;d是合金的平均晶粒尺寸(S1合金为84.58μm,S2合金为28.50μm),经计算,σg值:S1和S2合金分别为85MPa和146MPa
位错强化(σd)可以用以下公式来确定
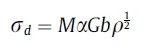
其中M是平均取向系数,对于FCC基体来说是3.06;α是一个常数,对于FCC基体来说等于0.2;G是剪切模量,对于Fe-36Ni Invar合金来说等于57GPa;b是伯氏矢量的大小(对于FCC基体来说是0.25787纳米);ρ是位错密度(S1合金为0.56×1014 m-2,S2合金为2.17×1014米m-2)。因此,S1和S2合金的σd计算值分别为67MPa和133MPa。
沉淀强化的屈服强度可以通过以下公式计算
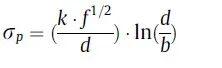
其中f和d分别是沉淀物的体积分数和平均直径。k是一个常数,其值为5.9 N/m,b是FCC的Burgers向量(0.25787 nm)。根据测量结果,S2合金中富含Zr的IMC的f和d为0.85 %和135 nm。通过沉淀强化计算,S2合金的屈服强度约为26Mpa。
除了Zr,S1和S2合金中的元素含量大致相等。然而,合金元素Zr在铁中的固溶度很小。因此,σs由下面公式表示
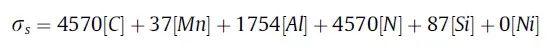
基于上述讨论,经计算,S1和S2 Fe-36Ni Invar合金的屈服强度分别为250MPa和395MPa。与σg和σd相比,σs和σp似乎可以忽略不计,因为Zr元素在基体中的固溶度可以忽略不计,而且富含Zr的IMC的比例相对较低,尺寸较大。因此,S2合金较高的强度主要归因于晶粒细化强化和位错强化。
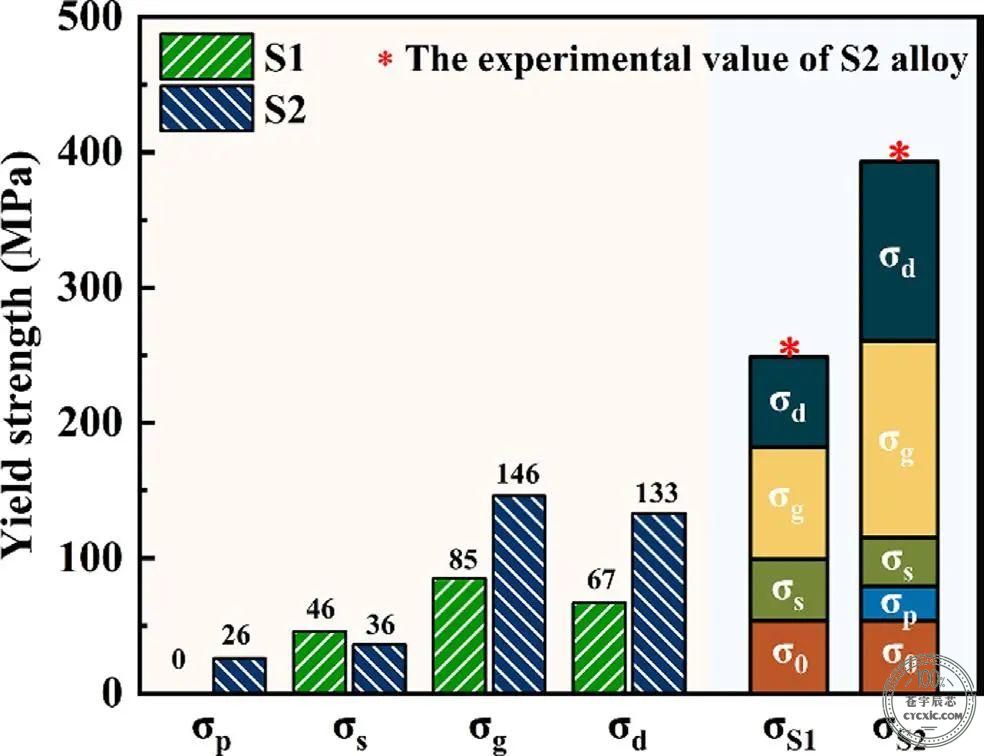
图6 来自不同强化机制的强度贡献
一般来说,电解双喷的薄区相对于离子减薄会更大一些,故优先考虑电解双喷制样方式。
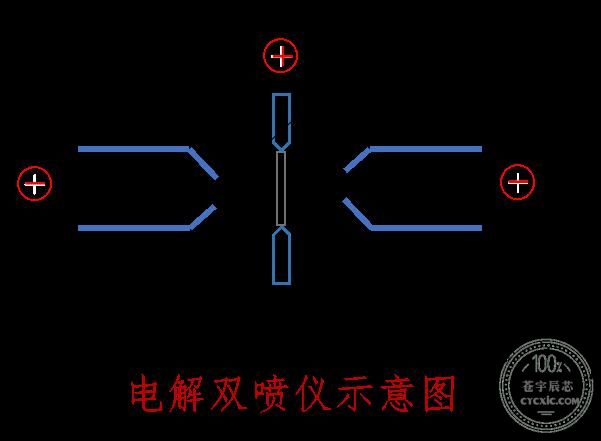
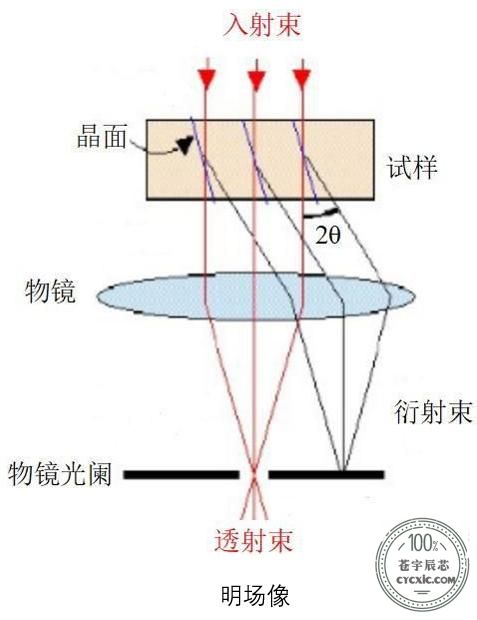
明场像(BF,必选项目)——使用透射电子束成像,观察富Zr相的组织形态
选区衍射(SAED,必选项目)——确认富Zr相类型
低指数高分辨像(HRTEM,必选项目)——进一步确认富Zr相
能谱面扫(Mapping,必选项目)——观察富Zr相元素分布
SAED标定——文章结合能谱与电子衍射确定Ni7Zr2、Ni2Zr沉淀相的存在,建议使用标定网址进行分析。